주식 투자를 하다 보면 기대수익률과 함께 표준편차라는 수치를 보는 일이 있습니다. 기대수익률은 많이 듣다 보니 대략 이해가 가지만 표준편차는 학창 시절 자주 들었던 것 같긴 한데 가물가물 합니다. 도대체 표준편차는 주식과 무슨 관계가 있는 걸까요?
목차
기대수익률 복습 좀 해볼까?
표준편차가 무슨 말이야?
그래서 주식이랑 표준 편차는 무슨 관계야?
무조건 표준편차가 낮은 곳에 투자를 하면 되는 거야?
기대수익률 복습 좀 해볼까?
기대수익률이라는 건 간단히 말하면 우리가 어떤 투자를 했을 때 이 정도 수익을 올릴 수 있을 것 같다는 예측치입니다. 그럼 기대수익률은 어떻게 구할까요? 일반적으로는 과거의 실적의 평균을 낸 값을 기대수익률로 봅니다.
예를 들어 아래의 주식A와 B가 있다면 두 주식의 기대수익률은 6%가 됩니다.
| 1년 | 2년 | 3년 | 4년 | 5년 | 6년 | |
| A 주식 | 6% | 6% | 6% | 6% | 6% | 6% |
| B 주식 | 12% | -6% | 4% | 18% | 0% | 8% |
A주식 기대수익률 = 6% = (6 + 6+ 6 + 6 + 6 _+ 6) ÷ 6
B주식 기대수익률 = 6% = (12 + (-6) + 4 + 18 + 0 + 8) ÷ 6
물론 실제 수익률은 기대수익률과 일치하지 않는 경우가 더 많습니다. 주식시장은 변동성이 매우 큰 편이기 때문입니다. 따라서 기대수익률 차제를 신뢰하기는 어렵습니다. 그래서 기대수익률과 함께 표준편차를 활용하면 비교적 더 정확하게 수익률의 범위를 예측해볼 수 있습니다.
표준편차가 무슨 말이야?
표준편차를 이해하려면 먼저 편차를 구할 수 있어야 합니다.
편차가 뭐야?
편차라는 것은 어떤 데이터셋(자료)이 있을 때 개별 데이터의 값과 평균의 차이를 의미합니다. 위의 A주식과 B주식을 다시 불러보겠습니다.
| 1년 | 2년 | 3년 | 4년 | 5년 | 6년 | |
| A 주식 | 6% | 6% | 6% | 6% | 6% | 6% |
| B 주식 | 12% | -6% | 4% | 18% | 0% | 8% |
A주식의 편차는 아래와 같이 구할 수 있습니다. 평균이 6%이고 개별 값 역시 모두 6%라서 다 0이 되어버리네요.
1년: 6 - 6 = 0
2년: 6 - 6 = 0
3년: 6 - 6 = 0
4년: 6 - 6 = 0
5년: 6 - 6 = 0
6년: 6 - 6 = 0
B주식의 편차는 아래와 같이 구할 수 있습니다. B의 경우 편차의 값이 다양하네요.
1년: 12 - 6 = 6
2년: -6 - 6 = -12
3년: 4 - 6 = -2
4년: 18 - 6 = 12
5년: 0 - 6 = -6
6년: 8 - 6 = 2
그래서 편차랑 표준편차는 무슨 관계야?
표준편차를 간단히 정의하면 '편차의 기준이 되는 값'이라고 할 수 있습니다. 표준편차를 보면 평균에서 멀리 떨어져 분포하는 값이 많은지 적은지 알 수 있습니다. 언뜻 생각해보면 편차를 다 더해서 편차 평균을 구해보면 될 것 같은데 평균을 다 더하면 0이 되어 버립니다.
B주식 편차의 합
6 + (-12) + (-2) + 12 + (-6) + 2 = 0
분산을 구하기
그래서 편차의 합의 평균 대신 편차를 제곱해서 다 더해서 평균을 구한 값을 활용하는데 이 값을 분산이라고 부릅니다.
(6 x 6) + (-12 x -12) + (-2 x -2) + (12 x 12) + (-6 x -6) + (2 x 2) = 368
368 ÷ 6 = 61.33333333....
이 분산이라는 값의 크기로도 대략적으로 평균에서 떨어져 있는 값이 많은지 적은지 알 수 있지만 아무래도 제곱을 했으니까 값이 엄청 커집니다. 단위도 %였던 것이 더 이상 %라고 하기 어려운 값이 됩니다. 그래서 실제로는 분산보다는 분산에 루트를 띄운 표준편차를 더 자주 이용합니다.
표준편차 구하기
표준편차는 분산에 루트를 씌어서 구합니다.
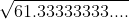
= 7.83156....
'7.83156....%'가 B 주식 기대수익률의 표준편차입니다.
그럼 A주식의 표준편차는 어느정도 될까요? 이미 눈치채셨겠지만 비교가 쉽도록 예를 매우 단순화해두었습니다. A주식의 경우 편차가 모두 0이기 때문에 분산도 표준편차도 0이 됩니다.
| 주식 | 기대수익률 | 표준편차 |
| A 주식 | 6% | 0% |
| B 주식 | 6% | 7.83156....% |
똑같이 기대수익률이 6%인 주식이지만 어느 주식에 투자하는 것이 더 위험해 보이나요?
| 1년 | 2년 | 3년 | 4년 | 5년 | 6년 | |
| A 주식 | 6% | 6% | 6% | 6% | 6% | 6% |
| B 주식 | 12% | -6% | 4% | 18% | 0% | 8% |
예를 단순화 해두었기 때문에 사실 표준편차까지 구하지 않아도 B주식 쪽이 훨씬 리스크가 크다는 것을 알 수 있습니다.
예를 통해서 알 수 있는 것처럼 표준편차의 크기를 통해서 투자자는 리스크를 어느 정도 파악할 수가 있습니다. 같은 6%의 기대수익률이지만 B주식에 투자를 하는 것은 A주식에 투자를 하는 것보다 훨씬 위험할 가능성이 높다는 것을 알 수 있습니다.
무조건 표준편차가 낮은 곳에 투자를 하면 되는 거야?
일단 표준편차를 낮추는 쪽이 리스크를 줄이는데는 큰 도움이 됩니다. 위의 예의 경우라면 일반적으로 A주식에 투자를 하는 쪽이 현명해 보입니다. 하지만 실제 주식시장에서는 A주식의 위험성은 실제로 0%가 아닙니다.
표준편차 자체가 자연 상태에서 주로 보이는 정규분포를 기준으로 하고 있기 때문에 변동성이 큰 주식시장을 제대로 표현하기는 어렵습니다. 자연 상태라면 정말 수억 년에 한 번 일어날까 말까 한 변동성이 주식시장에서는 5년에 한 번은 일어난다고 할 정도니까요.
또한 일반적으로 변동성이 작아서 표준편차가 작은 주식의 경우는 일반적으로 기대수익률도 낮은 경우가 많습니다. 아무리 로우 리스크라도 로우 리턴만 돌아온다면 수익률을 높이기 어려워집니다. 예를 들어서 10%이상의 수익률을 얻을 가능성을 따져본다면 B주식 쪽이 확률이 훨씬 높습니다.
따라서 기대수익률을 극대화하고 표준편차를 최소화할 수 있는 적절한 지점을 찾아서 포트폴리오를 구성라려고 노력하는 것이 투자자가 할 수 있는 최선이라고 할 수 있습니다.
함께 읽으면 좋은 글
평균의 함정이란? | 피하는 방법 (평균값, 중앙값, 최빈값)
5가지 수치 요약( 5 number summary) | 5수요약
은퇴 자금 얼마나 필요할까? | 파이어 족 | 금액 | 자산 규모






